統計分析のPython 実現ガイド
【概要】Pandas、SciPy、Matplotlibを用いた統計分析のPython実装ガイドである。記述統計量、ヒストグラム、箱ひげ図、クロス集計表、t検定、一元配置分散分析、正規性検定の7つの統計手法を解説し、各手法のPythonコードと実行結果を示す。データの特徴把握から仮説検証までの分析プロセスを網羅する。
【目次】
【サイト内のPython関連主要ページ】
- Windows AI支援Python開発環境構築ガイド: 別ページ »で説明
- AIエディタ Windsurf の活用: 別ページ »で説明
- AIエディタCursorガイド: 別ページ »で説明
- Google Colaboratory: 別ページ »で説明
- Python(Google Colaboratoryを含む)のまとめ: 別ページ »で説明
- 機械学習の Python 実現ガイド: 別ページ »で説明
- 行列計算の Python 実現ガイド: 別ページ »で説明
- 統計分析のPython での実現ガイド: 別ページ »で説明
- 音声信号処理の Python 実現ガイド: 別ページ »で説明
- カラー画像処理の Python 実現ガイド: 別ページ »で説明
- Python 言語によるとても簡単なアドベンチャーゲーム(変数,式,if,while,関数,print,time.sleep, def, global を使用): 別ページ »で説明
- Pythonプログラミング講座:基礎から応用まで(授業資料,全15回): 別ページ »で説明
- Pythonプログラミングの例と実践ガイド: 別ページ »で説明
【外部リソース】
- Pythonの公式サイト: https://www.python.org
- 東京大学の「Pythonプログラミング入門」: https://utokyo-ipp.github.io/IPP_textbook.pdf
- ITmedia社の「Pythonチートシート」の記事: https://atmarkit.itmedia.co.jp/ait/articles/2004/20/news015.html
統計手法
- 記述統計量
- ヒストグラム
- クロス集計表
- 検定
記述統計量
記述統計量は、データセットの特徴を数値的に要約する統計指標である。データ全体の特性を把握し、適切な分析手法の選択を支援する。
基本的な統計量として以下が挙げられる。
- 平均値(データの中心傾向を示す指標)
- 標準偏差(データのばらつきを定量化する統計量)
- 中央値(データの中心的傾向を示す指標)
- 四分位点(分布の形状を特徴付ける統計量)
- 最大値(データセットの上限を示す値)
- 最小値(データセットの下限を示す値)
- 分散(データの変動性を定量化する指標)
- 歪度(分布の非対称性を評価する統計量)
- 尖度(分布の尖り具合を示す統計量)
用語リスト
- 記述統計量: データ分析の基本となる数値指標の総称である。平均値、標準偏差、中央値などの基本統計量を含み、データの特徴を把握するための手法である。
- 平均値: データの総和をデータ数で除した代表値であり、データ分布の中心的傾向を示す基本的な統計量である。外れ値の影響を受けやすいため、データの性質に応じた適切な解釈が必要である。
- 標準偏差: データのばらつきを定量化する指標であり、平均値からの平均的な距離を表す。この値が大きいほどデータの変動性が高いことを示す。
- 中央値: 順序付けられたデータの中央に位置する値であり、外れ値の影響を受けにくい特性を持つ。非対称な分布において有効な代表値として機能する。
- 四分位数: データを4等分する境界値であり、第1四分位数、中央値、第3四分位数から構成される。分布形状の把握と外れ値の検出に役割を果たす。
- 最大値: データセット内の最高値を示す基本統計量であり、データの範囲把握と外れ値の検出に活用される。
- 最小値: データセット内の最低値を示す基本統計量であり、データの範囲把握と外れ値の検出に活用される。
- 分散: データの散らばりを表す統計量であり、各データ点と平均値の差の二乗平均として定義される。標準偏差の二乗値として表される。
- 歪度: 分布の非対称性を定量化する指標であり、正規分布では0となる。正値は右側に、負値は左側に裾が長い分布を示す。
- 尖度: 分布の尖り具合を示す指標であり、正規分布を基準(3)として評価される。値が大きいほど尖った分布、小さいほど平坦な分布を表す。
- pandas: データ分析を実現するPythonライブラリであり、記述統計量の計算や多様なデータ処理機能を提供する。describeメソッドにより主要な統計量を算出できる。
- 属性: データベースやデータフレームにおける各列の特性を表す要素であり、分析対象データの特徴を示す情報である。
- データフレーム: 行と列で構成される2次元のデータ構造であり、pandasライブラリの中核機能として提供される。複数の属性と観測値を管理する。
- 外れ値: データセット内で他のデータから著しく離れた値であり、統計分析結果に影響を及ぼす可能性がある。適切な処理方法の選択が分析の精度を決定する。
- 分布: データの散らばり方や偏りを示す概念であり、記述統計量によってその特徴を数値的に把握する。
- ヒストグラム: データの分布を視覚的に表現する統計グラフであり、データの範囲を区間分割し、各区間の頻度を棒グラフで表示する。分布の形状や特徴を直感的に理解するための可視化手法である。
- クロス集計表: 2つの変数間の関係性を表形式で示す分析ツールであり、変数間の関連性を把握するための基本的手法である。行と列の変数の組み合わせごとの度数を表示する。
- t検定: 2群の平均値の差の統計的有意性を評価する検定手法であり、帰無仮説「母集団の平均が等しい」に対してp値を算出し、有意水準との比較により判断を可能にする。
- Welchのt検定: 分散が等しくない2群の比較に最適化されたt検定の発展形であり、等分散を仮定しないため、より広範な状況で信頼性の高い検定を実現する。
- ノンパラメトリック検定: 母集団分布の特定の形状を仮定しない検定手法であり、順位や符号を用いて検定を実施する。データの分布に依存しない特徴を持つ統計手法である。
- 一元配置分散分析: 3群以上の平均値の差を同時に検定する統計手法であり、複数群間の差を比較し、p値により統計的有意性を判断する。多群間比較における基本的な分析ツールとして広く活用される。
- Shapiro-Wilk検定: データの正規性を評価する検定手法であり、帰無仮説「母集団が正規分布である」に対してp値を算出し、分布の特性を統計的に判断する。
- p値: 統計的検定において、帰無仮説が真である場合に観測データが得られる確率を示す指標であり、一般的に5%未満を統計的有意として、仮説検定の判断基準として広く採用される。
- データ分析: 収集されたデータから有用な情報や知見を抽出する体系的なプロセスであり、記述統計量の算出は、この過程における初期段階として、分析全体の方向性を決定付ける役割を果たす。
- 統計指標: データの特徴を数値化して表現する指標であり、記述統計量はその代表的な例として、データの性質や傾向を客観的に評価するための基準として機能する。
統計処理の比較
| 処理内容 | SPSS言語 | Rシステム | Python (pandas/scipy) |
|---|---|---|---|
| 記述統計量 | describe、skew、kurt descriptive |
summary、sd、skewness、kurtosis |
df.describe()、stats.skew()、stats.kurtosis() |
| 頻度表 | hist、frequencies |
table |
value_counts() |
| クロス集計表 | crosstab、crosstabs |
table |
pd.crosstab() |
| 集約 | aggregate |
aggregate |
groupby().agg() |
| Welchのt検定 | ttest_ind |
t.test |
stats.ttest_ind() |
| 一元配置分散分析 | f_oneway |
oneway.test |
stats.f_oneway() |
| Wilcoxon検定 | mannwhitneyu |
wilcox.test |
stats.mannwhitneyu() |
Pythonプログラム例
データセット構造
| 科目 | 受講者 | 得点 |
|---|---|---|
| 国語 | A | 90 |
| 国語 | B | 80 |
| 算数 | A | 95 |
| 算数 | B | 90 |
| 理科 | A | 80 |
Pythonのインストールと必要なPythonライブラリのインストール(Windows上)
- Pythonのインストール
注:既にPython(バージョン3.12を推奨)がインストール済みの場合は、この手順は不要である。
winget(Windowsパッケージマネージャー)を使用してインストールを行う。
- Windowsで、コマンドプロンプトを管理者権限で起動する(手順: Windowsキーまたはスタートメニュー、「cmd」と入力、右クリックメニューなどで「管理者として実行」を選択)。
- winget(Windowsパッケージマネージャー)が利用可能か確認する。
winget --version
- Pythonのインストール(下のコマンドによりPython 3.12がインストールされる)。
reg add "HKLM\SYSTEM\CurrentControlSet\Control\FileSystem" /v LongPathsEnabled /t REG_DWORD /d 1 /f REM Python をシステム領域にインストール winget install --scope machine --id Python.Python.3.12 -e --silent REM Python のパス set "INSTALL_PATH=C:\Program Files\Python312" echo "%PATH%" | find /i "%INSTALL_PATH%" >nul if errorlevel 1 setx PATH "%PATH%;%INSTALL_PATH%" /M >nul echo "%PATH%" | find /i "%INSTALL_PATH%\Scripts" >nul if errorlevel 1 setx PATH "%PATH%;%INSTALL_PATH%\Scripts" /M >nul
- 必要なPythonライブラリのインストール
【関連する外部ページ】
【サイト内の関連ページ】
基本的なデータ構造とデータフレームの作成
Pandasライブラリを活用し、科目・受講者・得点の成績データを辞書として作成し、データフレームへと変換する。データ型は、データ処理を実現するため、カテゴリ型と整数型を明示的に指定する。
- データ作成: 辞書「data」に、科目、受講者、得点のデータを格納する。
- データフレームの構築: pd.DataFrame(data)でデータフレームに変換する。
- データ型の明示的な指定: astype()を用いて、「科目」と「受講者」をカテゴリ型('category')に、「得点」を整数型('int32')に変換する。
import pandas as pd
# データの作成
data = {
'科目': ['国語', '国語', '算数', '算数', '理科'],
'受講者': ['A', 'B', 'A', 'B', 'A'],
'得点': [90, 80, 95, 90, 80]
}
# データフレームの作成
df = pd.DataFrame(data)
# データ型の明示的な指定
df = df.astype({
'科目': 'category',
'受講者': 'category',
'得点': 'int32'
})
print("基本データ:")
print(df)
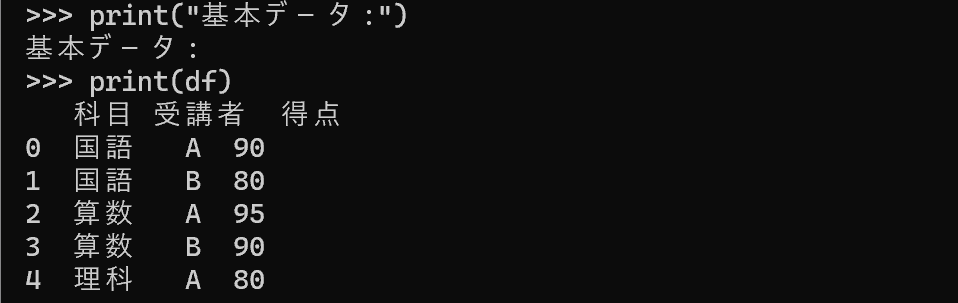
個別の統計量計算
Pandasとscipy.statsの統計関数を活用し、カテゴリカルデータと数値データを含むデータフレームに対して平均値、標準偏差、四分位数などの基本統計量を算出する。標本標準偏差の計算にはddof=1を指定し、結果の小数点以下の桁数を適切に設定する。
- 「科目」と「受講者」列をカテゴリ型に変換する。「得点」列を整数型(int32)に変換する。
- 「得点」に対して、平均、標準偏差、中央値、最大値、最小値、四分位数(第1および第3)を算出する。SciPyを用いて歪度と尖度を算出する。
- ddof=1を指定することにより標本標準偏差を算出する。
import pandas as pd
from scipy import stats
# データの作成
data = {
'科目': ['国語', '国語', '算数', '算数', '理科'],
'受講者': ['A', 'B', 'A', 'B', 'A'],
'得点': [90, 80, 95, 90, 80]
}
# データフレームの作成
df = pd.DataFrame(data)
# データ型の明示的な指定
df = df.astype({
'科目': 'category',
'受講者': 'category',
'得点': 'int32'
})
# 基本統計量の個別計算
scores = df['得点']
# 標本標準偏差の計算(ddof=1指定)
print("基本統計量:")
print(f"平均値: {scores.mean():.1f}")
print(f"標準偏差: {scores.std(ddof=1):.1f}")
print(f"中央値: {scores.median():.1f}")
print(f"最大値: {scores.max()}")
print(f"最小値: {scores.min()}")
print(f"第1四分位数: {scores.quantile(0.25):.1f}")
print(f"第3四分位数: {scores.quantile(0.75):.1f}")
print(f"歪度: {stats.skew(scores):.3f}")
print(f"尖度: {stats.kurtosis(scores):.3f}")
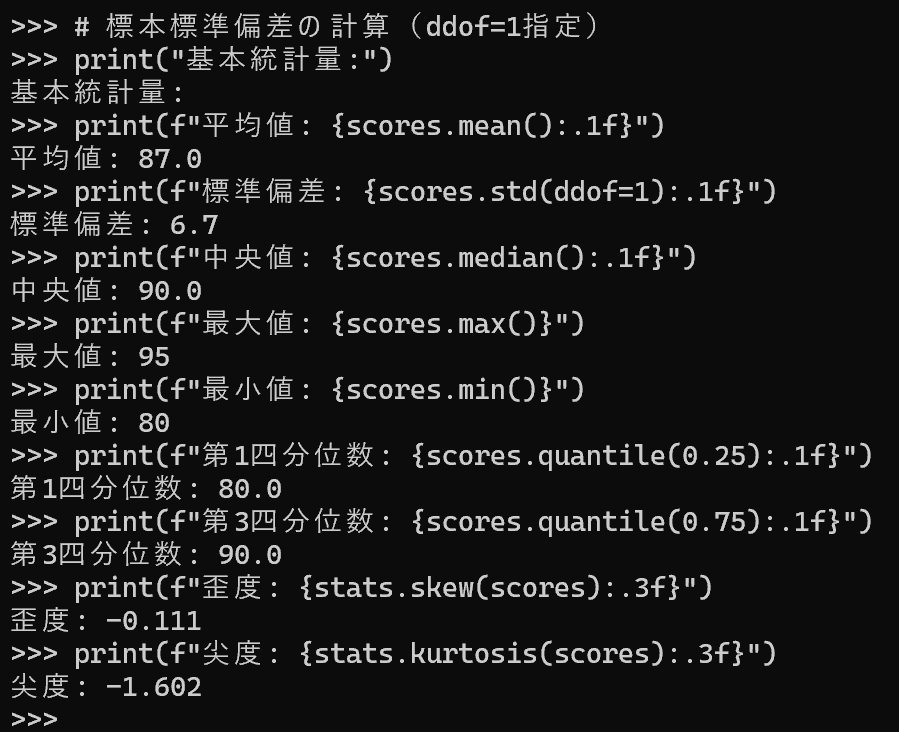
総合的な統計分析
Pandasライブラリのdescribeメソッドを活用し、データフレームの統計分析を実行する。データ数、平均値、標準偏差、最小値、四分位数、最大値などの基本統計量を算出し、データの特徴を把握する。
- データ型の適正化: 「科目」と「受講者」列をカテゴリ型に、「得点」列を整数型(int32)に変換することで処理効率を向上させる。
- 総合分析: describe()メソッドにより、全体の得点データの基本統計量を一括で算出し、データの全体像を把握する。
- カテゴリ別分析: groupby()メソッドとdescribe()メソッドを組み合わせ、科目ごとの詳細な統計量を算出する。
import pandas as pd
# データの作成
data = {
'科目': ['国語', '国語', '算数', '算数', '理科'],
'受講者': ['A', 'B', 'A', 'B', 'A'],
'得点': [90, 80, 95, 90, 80]
}
# データフレームの作成
df = pd.DataFrame(data)
# データ型の明示的な指定
df = df.astype({
'科目': 'category',
'受講者': 'category',
'得点': 'int32'
})
# describe()メソッドによる総合的な統計量の算出
# count:データ数、mean:平均、std:標準偏差、min:最小値、25%:第1四分位、50%:中央値、75%:第3四分位、max:最大値
print("\n総合的な統計量:")
print(df['得点'].describe())
# 科目別の統計量
# groupby()で科目ごとにグループ化し、describe()で各グループの統計量を算出
print("\n科目別の統計量:")
print(df.groupby('科目')['得点'].describe())
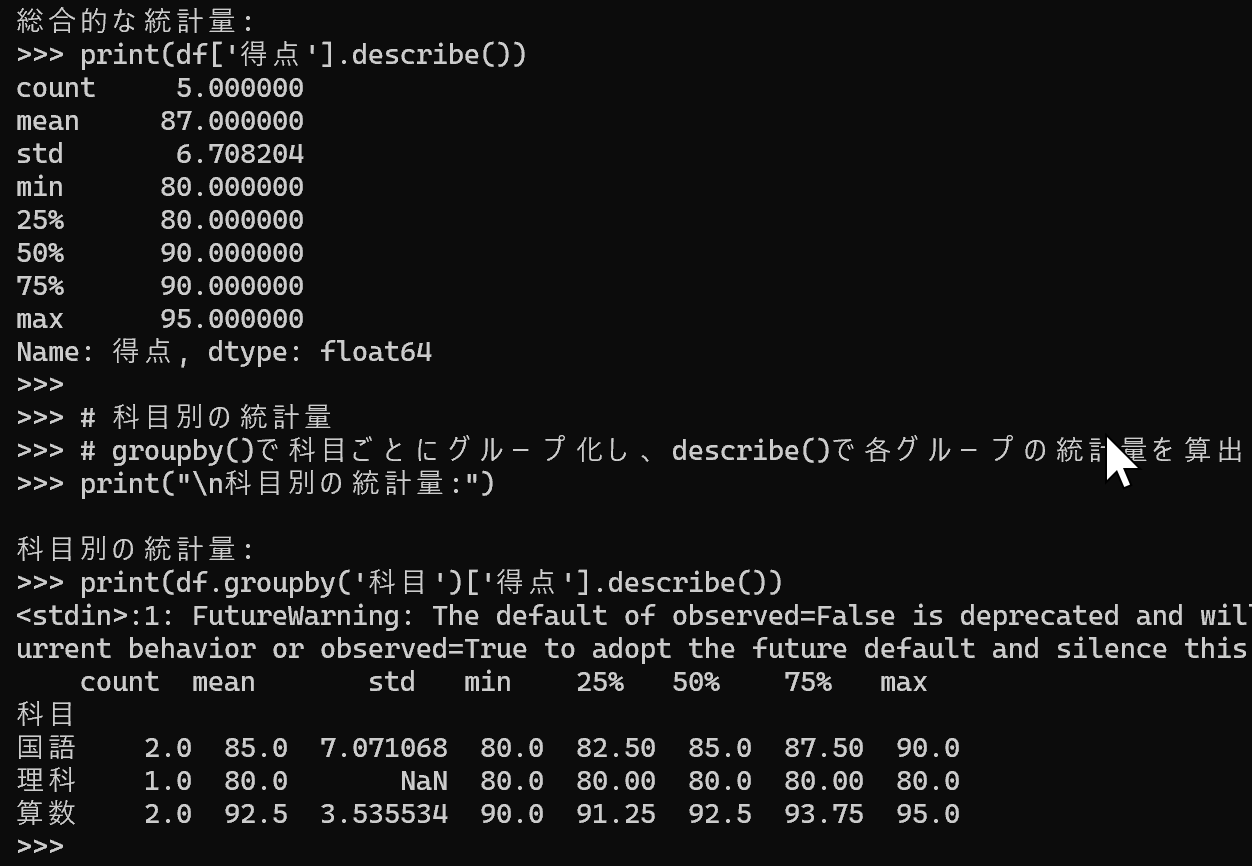
データの可視化、ヒストグラム
Matplotlibを活用し、統計データの視覚的な理解を促進する箱ひげ図とヒストグラムを生成する。japanize_matplotlibによる日本語表示対応、グリッド線の追加、軸ラベルの設定などにより、直感的な分析を可能にする。
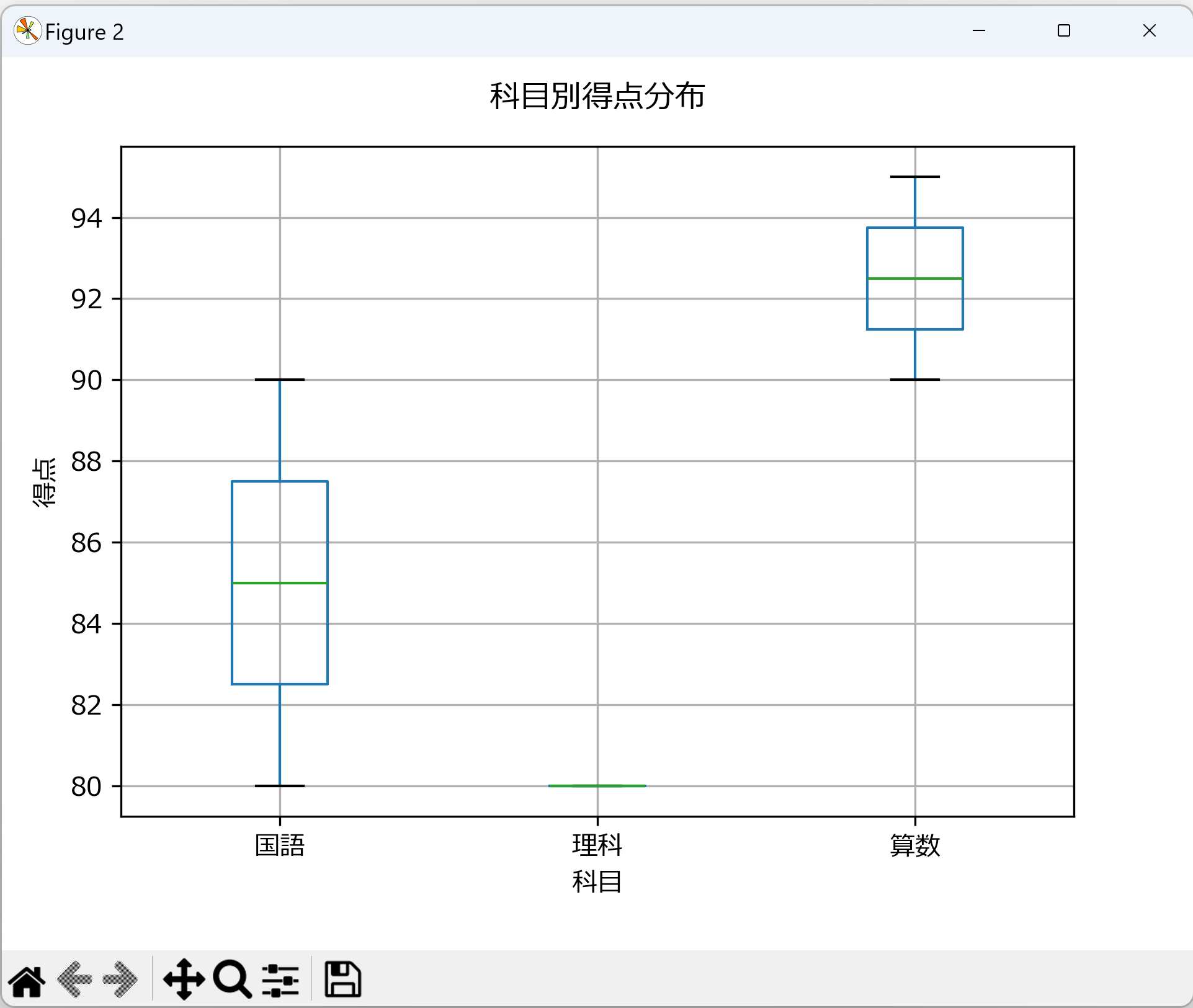
- 箱ひげ図の生成: Pandasのboxplotメソッドを使用し、カテゴリ(科目)ごとの得点分布を可視化する。plt.figureで図の大きさを設定し、グリッド線、軸ラベル、タイトルを配置する。
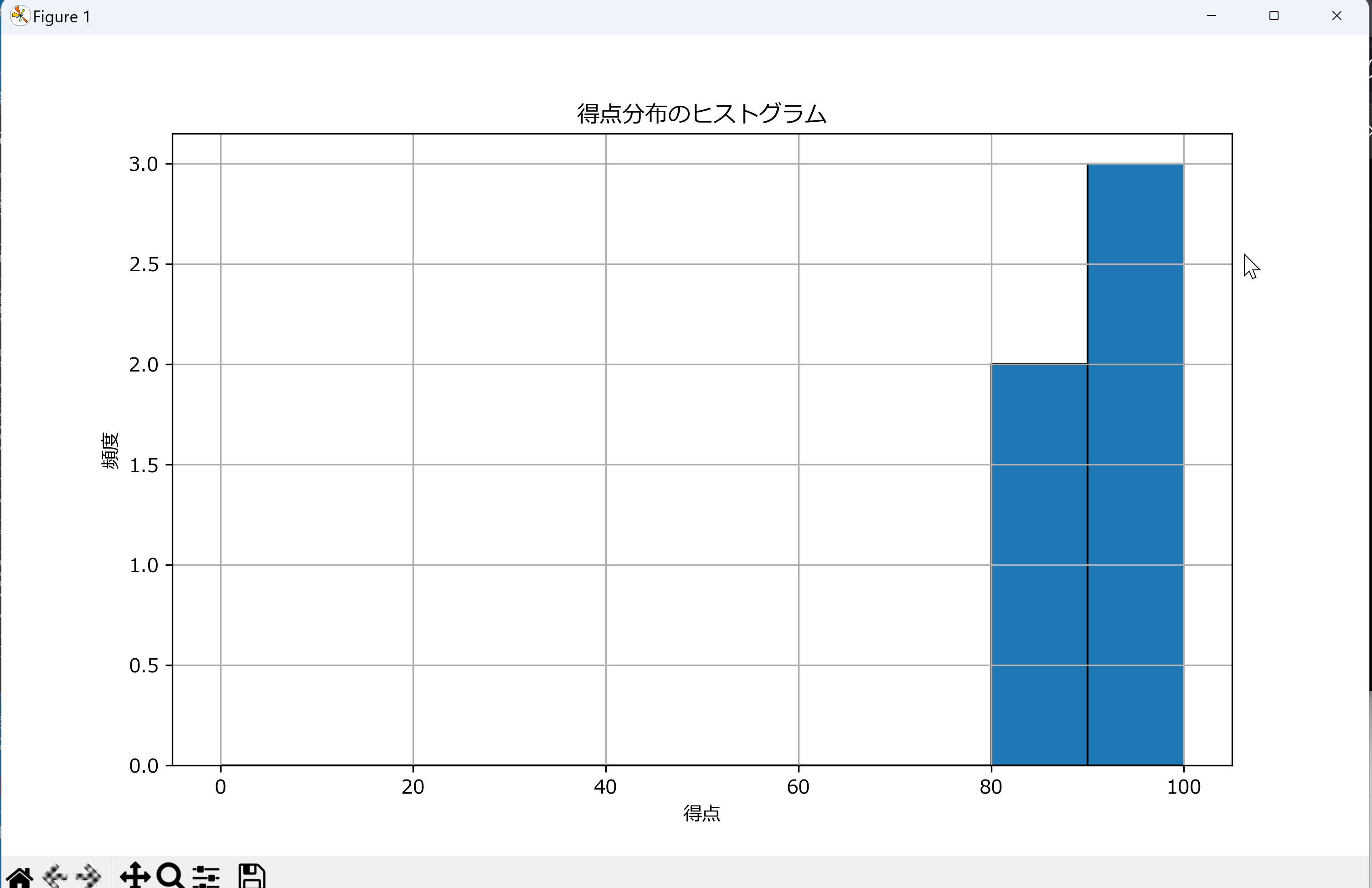
- ヒストグラムの作成: plt.histを活用し、得点分布を0~100の範囲で10刻みの帯として表示する。エッジカラーを黒に指定し、各区間の境界を明確化する。
- 出力の最適化: タイトル、軸ラベル、グリッド線を追加し、データの特徴を直感的に理解できるよう工夫する。
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib # 日本語表示用
import platform
# OSがWindowsの場合のみフォントを設定
if platform.system() == 'Windows':
plt.rcParams['font.family'] = 'Meiryo'
# データの作成
data = {
'科目': ['国語', '国語', '算数', '算数', '理科'],
'受講者': ['A', 'B', 'A', 'B', 'A'],
'得点': [90, 80, 95, 90, 80]
}
# データフレームの作成
df = pd.DataFrame(data)
# データ型の明示的な指定
df = df.astype({
'科目': 'category',
'受講者': 'category',
'得点': 'int32'
})
# 箱ひげ図の作成
plt.figure(figsize=(10, 6))
df.boxplot(column='得点', by='科目')
plt.suptitle('') # 自動で付加されるサブタイトルを削除
plt.title('科目別得点分布', pad=15) # タイトルの余白調整
plt.ylabel('得点')
plt.grid(True)
plt.savefig('score_distribution.png', bbox_inches='tight') # 画像を保存
plt.show() # 画面に表示
plt.close() # 描画後にクローズ
# ヒストグラムの作成
plt.figure(figsize=(10, 6))
plt.hist(df['得点'], bins=range(0, 101, 10), edgecolor='black') # binの範囲を0-100に設定
plt.title('得点分布のヒストグラム')
plt.xlabel('得点')
plt.ylabel('頻度')
plt.grid(True)
plt.savefig('score_histogram.png', bbox_inches='tight') # 画像を保存
plt.show() # 画面に表示
plt.close() # 描画後にクローズ
クロス集計表の例
Pandasのcrosstabを活用し、二つの変数間の関係性を表形式で示すクロス集計表を作成する。クロス集計表は、複数のグループの組み合わせごとの出現頻度を整理し、データの分布や傾向を把握することを可能にする。
- クロス集計の実装: pd.crosstab関数を使用し、DataFrameの「グループ1」の値を行インデックス、「グループ2」の値を列インデックスとして、各組み合わせの出現頻度を算出する。
- データの可視化: クロス集計表により、グループごとの頻度を表形式で整理し、データの特徴を把握する。
import pandas as pd
# データセットサンプルの作成
data = {
'グループ1': ['a', 'b', 'c', 'a', 'b'],
'グループ2': ['d', 'd', 'e', 'e', 'e']
}
df = pd.DataFrame(data)
# クロス集計表の作成
# crosstabは2つの系列間でグループ単位での頻度(出現回数)を集計する
# index=行インデックス, columns=列インデックスを指定
cross_table = pd.crosstab(df['グループ1'], df['グループ2'])
print(cross_table)
# (Optional) 行・列の合計を含めたい場合は、margins=True を指定
cross_table_with_margins = pd.crosstab(df['グループ1'], df['グループ2'], margins=True)
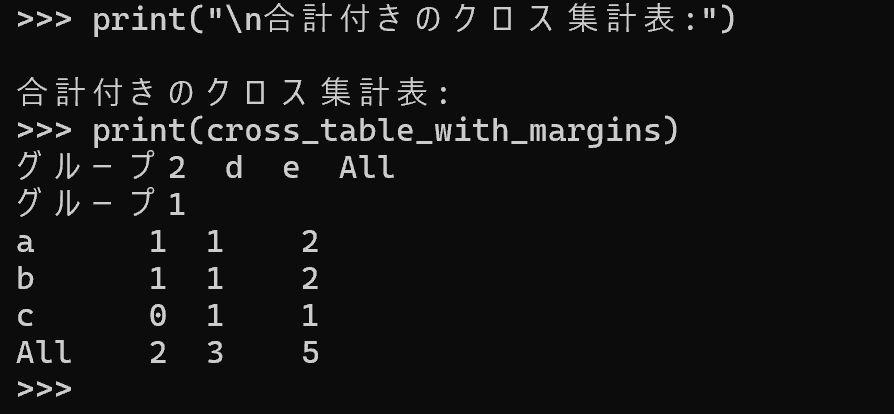
print("\n合計付きのクロス集計表:")
print(cross_table_with_margins)
t検定
SciPyのstatsモジュールを活用し、2群間の平均値の差を検定するWelchのt検定を実装する。再現性を確保するために乱数のシード値を固定し、異なる平均値を持つ正規分布からサンプルデータを生成して、等分散を仮定しない検定を実行する。
- サンプルデータの生成: numpyを用いて正規分布から2群のサンプルデータを生成する。
- 再現性の確保: np.random.seed(42)により乱数生成のシードを固定し、結果の再現性を担保する。
- 検定の実施: SciPyのstatsモジュールのttest_ind関数をequal_var=Falseオプションで使用し、Welchのt検定を実行する。
import numpy as np
from scipy import stats
# シード値を固定して再現性を確保
np.random.seed(42)
# 2群のサンプルデータを正規分布から生成
# group1: 平均0、標準偏差1の正規分布から100個
# group2: 平均0.5、標準偏差1の正規分布から100個
group1 = np.random.normal(0, 1, 100)
group2 = np.random.normal(0.5, 1, 100)
# Welchのt検定を実行
# equal_var=Falseで分散が等しくないことを仮定
# 戻り値はt統計量とp値のタプル
t_stat, p_value = stats.ttest_ind(group1, group2, equal_var=False)
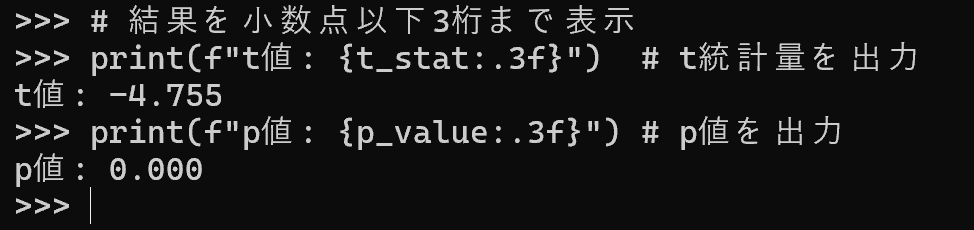
# 結果を小数点以下3桁まで表示
print(f"t値: {t_stat:.3f}") # t統計量を出力
print(f"p値: {p_value:.3f}") # p値を出力
一元配置分散分析
SciPyの統計解析機能を活用し、一元配置分散分析により3群以上のデータ群の平均値の差を統計的に検定する。F値とp値を算出し、群間の差異を評価する。
- 分析の実装: SciPyライブラリのstatsモジュールを用いて、一元配置分散分析(One-way ANOVA)を実行する。
- データ構造の準備: グループA、B、Cの3群それぞれの測定値リストを準備し、各群の母平均の同一性を検証する。
- 統計量の算出: stats.f_oneway()関数により、3群以上の群間差をF統計量とp値を用いて評価する。
from scipy import stats
# サンプルデータ(数値のグループ別データ)
group_a = [3.42, 3.84, 3.96, 3.76] # グループAの測定値
group_b = [3.17, 3.63, 3.47, 3.44, 3.39] # グループBの測定値
group_c = [3.64, 3.72, 3.91] # グループCの測定値
# 一元配置分散分析の実行
f_stat, p_value = stats.f_oneway(group_a, group_b, group_c)
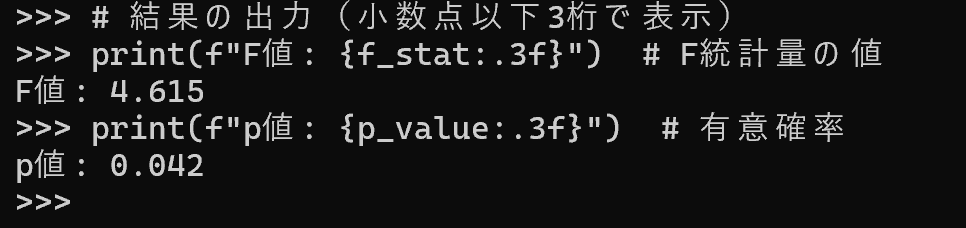
# 結果の出力(小数点以下3桁で表示)
print(f"F値: {f_stat:.3f}") # F統計量の値
print(f"p値: {p_value:.3f}") # 有意確率
正規性の検定
Shapiro-Wilk検定を活用し、データの正規性を統計的に評価する。正規分布に従うサンプルデータを生成して検定統計量とp値を算出し、データが正規分布に従うという帰無仮説を検証する。
- 検定の実装: SciPyのstatsモジュールを用いてShapiro-Wilk検定を実行し、データの正規性を評価する。
- データ生成: NumPyを活用して正規分布(平均0、標準偏差1)に従う100個のサンプルデータを生成する。
- 再現性の確保: np.random.seed(42)により乱数生成のシードを固定し、結果の再現性を担保する。
from scipy import stats
import numpy as np
# データ生成:平均0、標準偏差1の正規分布から100個のサンプルを生成
np.random.seed(42)
data = np.random.normal(0, 1, 100)
# Shapiro-Wilk検定の実行
# 帰無仮説:データは正規分布に従う
stat, p_value = stats.shapiro(data)
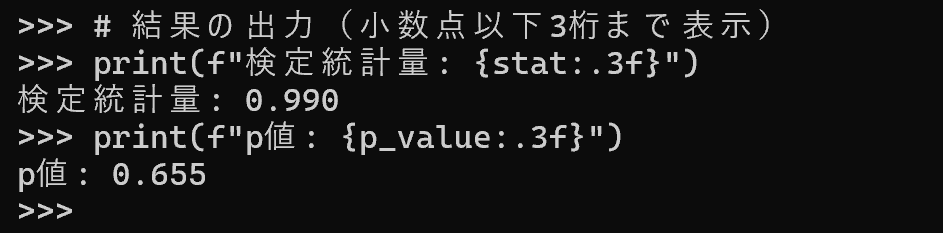
# 結果の出力(小数点以下3桁まで表示)
print(f"検定統計量: {stat:.3f}")
print(f"p値: {p_value:.3f}")
![[kaneko lab.]](https://www.kkaneko.jp/info/logo_png.png)